де x – аргумент; с, b - константи.
Якщо зокрема, k=0, то одержуємо сталу функцію y=b;
якщо b=0, то одержуємо пряму пропорційність y=kx.
Властивості функції y=kx+b:
1. Область визначення - множина всіх дійсних чисел
2. Функція y=kx+b загального виду, тобто ні парна, ні непарна.
3. При k>0 функція зростає, а при k<0 спадає на всій числовій осі.
Графіком функції є пряма.
Наприклад, задано функцію y = 2x + 1.
Розглянемо частинні випадки побудови графіків цієї функції:
1. Побудувати графік функції y = bx – графік прямої пропорційності, який є частинним випадком рівняння
y = kx + b, якщо b = 0.
Згідно з прикладом слід побудувати графік функції y = 2x.
Графіком є пряма лінія, що утворює з віссю абсцис кут α, такий що:
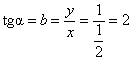
2. Побудувати графік функції y = c (це частинний вид рівняння y = kx + b, який b = 0), тобто побудувати графік функції y = 1.
Графіком є пряма лінія, паралельна до вісі абсцис.

3. Побудувати графік функції y = kx + b, тобто згідно з прикладом – графік функції y = 2x + 1.
Графіком є пряма лінія, що утворює з віссю абсцис кут α.
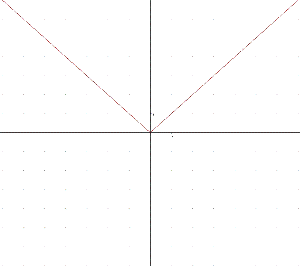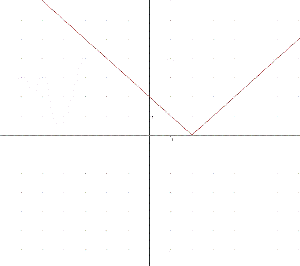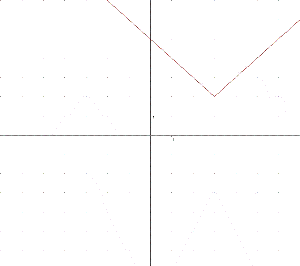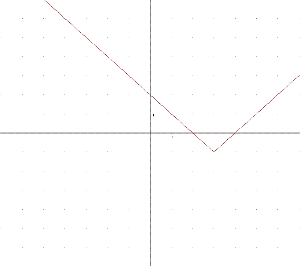
А ось функція у=|х=a|+b