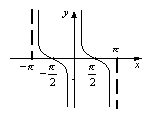
Тригонометрична функція задана формулою y=sinх
Властивості функції y=sinх:
1. Область визначення - проміжок (-∞;+∞).
2. Область значень – проміжок [-1;1].
3. Функція непарна, періодична з періодом Т=2П.
4. Функція зростає при -П/2+2Пn<х<П/2+2Пn, n є Z.
5. Функція спадає при П/2+2Пn<х<3П/2+2Пn, n є Z.
6. Функція має максимум у точках (П/2+2Пn;0), мінімум у точках (-П/2+2Пn;0), nє Z.
Властивості функції y=sinх:
1. Область визначення - проміжок (-∞;+∞).
2. Область значень – проміжок [-1;1].
3. Функція непарна, періодична з періодом Т=2П.
4. Функція зростає при -П/2+2Пn<х<П/2+2Пn, n є Z.
5. Функція спадає при П/2+2Пn<х<3П/2+2Пn, n є Z.
6. Функція має максимум у точках (П/2+2Пn;0), мінімум у точках (-П/2+2Пn;0), nє Z.
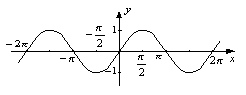
Тригонометрична функція задана формулою y=cosх
Властивості функції y=cosх:
1. Обл. визначення - проміжок (-∞;+∞).
2. Область значень – проміжок [-1;1].
3. Функція парна, періодична з періодом Т=2П.
4. Функція зростає при -П+2Пn<х<2Пn, nє Z.
5. Функція спадає при 2Пn<х<П+2Пn, nє Z.
6. Функція має максимум у точках (2Пn;0), мінімум у точках (П+2Пn;0), nєZ.
Властивості функції y=cosх:
1. Обл. визначення - проміжок (-∞;+∞).
2. Область значень – проміжок [-1;1].
3. Функція парна, періодична з періодом Т=2П.
4. Функція зростає при -П+2Пn<х<2Пn, nє Z.
5. Функція спадає при 2Пn<х<П+2Пn, nє Z.
6. Функція має максимум у точках (2Пn;0), мінімум у точках (П+2Пn;0), nєZ.
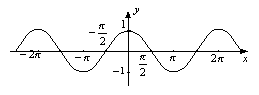
Тригонометрична функція задана формулою y=tgх
Властивості функції y=tgх:
1. Обл. визначення – всі дійсні числа, крім точок (П/2+2Пn), nєZ.
2. Область значень – проміжок (-∞;+∞).
3. Функція непарна, періо-дична з періодом Т= П.
4. Нулі функції – точки (Пn;0), nєZ.
5. Функція зростає на всій області визначення.
6. Функція не має екстремумів.
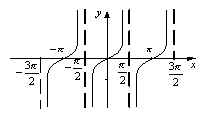
Тригонометрична функція задана формулою y=ctgх
Властивості функції y=ctgх:
Властивості функції y=ctgх: